Imagine in our manifold a very small closed loop whose four sides are
the coordinate lines 
, 
, 
,
.
Figure 6.3: Parallel transport around a closed loop ABCD.
A vector 
defined at A is parallel transported to B.
From the parallel transport law
it follows that at B the vector has components
where the notation `` '' under the integral denotes the path
AB. Similar transport from B to C to D gives
and
The integral in the last equation has a different sign because of the
direction of transport from C to D is in the negative 
direction.
Similarly, the completion of the loop gives
The net change in 
is a vector 
,
found by adding (93)-(96).
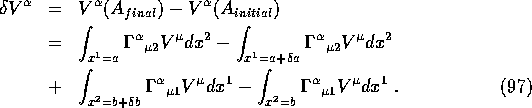
To lowest order we get
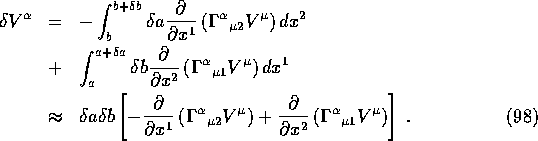
This involves derivatives of 
's and of 
. The
derivatives of can be eliminated using for example
This gives
To obtain this, one needs to relabel dummy indices in the terms
quadratic in .
Notice that this just turns out to be a number times 
summed on 
. Now the indices 1 and 2 appear because the
path was chosen to go along those coordinates. It is antisymmetric in
1 and 2 because the change would have the
opposite sign if one went around the loop in the opposite direction.
If we use general coordinate lines 
and 
, we
find
Defining
we can write
are the components of a 1/3 tensor.
This tensor is called the Riemann curvature tensor .
